
Motion in a straight line: Position-time graph, speed, and velocity. Least count, accuracy and precision of measuring instruments, Errors in measurement, Dimensions of Physical quantities, dimensional analysis, and its applications,įrame of reference.
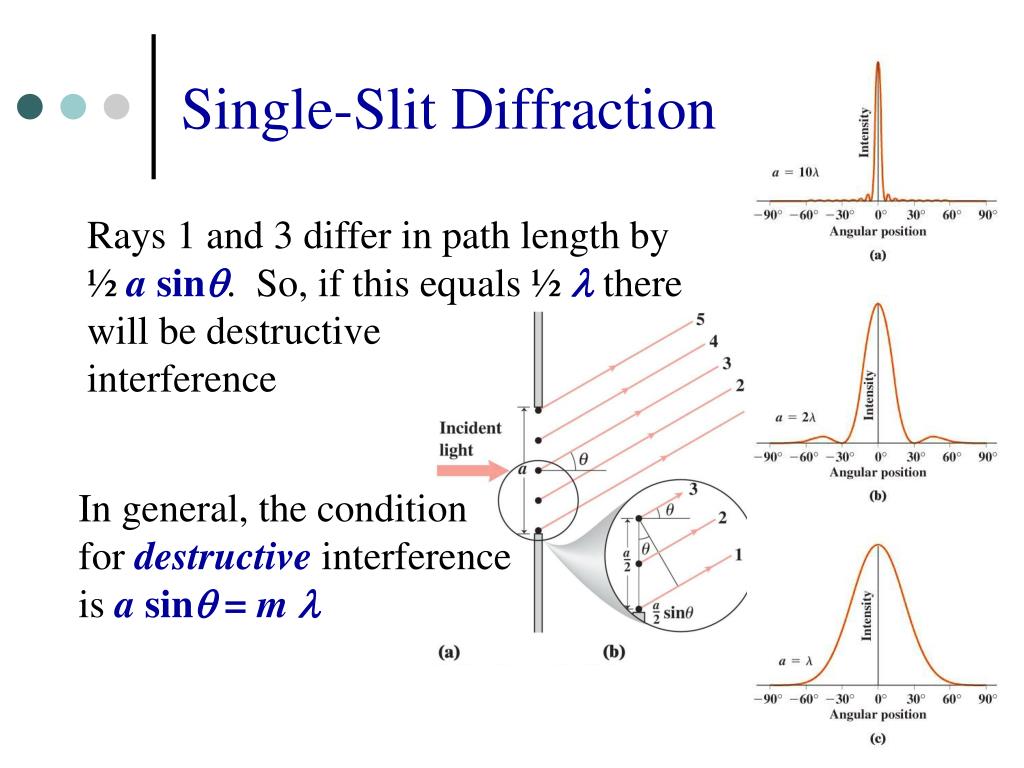
Physics, technology, and society, SI units, Fundamental and derived units. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License. Use the information below to generate a citation. Then you must include on every digital page view the following attribution: If you are redistributing all or part of this book in a digital format, Then you must include on every physical page the following attribution: If you are redistributing all or part of this book in a print format, Want to cite, share, or modify this book? This book uses the It is a product of the interference pattern of waves from separate slits and the diffraction of waves from within one slit. The solid line with multiple peaks of various heights is the intensity observed on the screen. One example of a diffraction pattern on the screen is shown in Figure 4.11. We refer to such a missing peak as a missing order. This gives rise to a complicated pattern on the screen, in which some of the maxima of interference from the two slits are missing if the maximum of the interference is in the same direction as the minimum of the diffraction. Interference and diffraction effects operate simultaneously and generally produce minima at different angles.
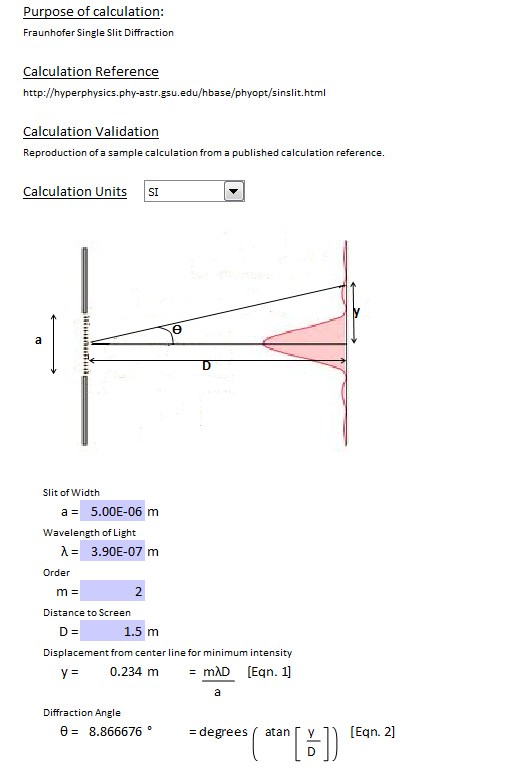
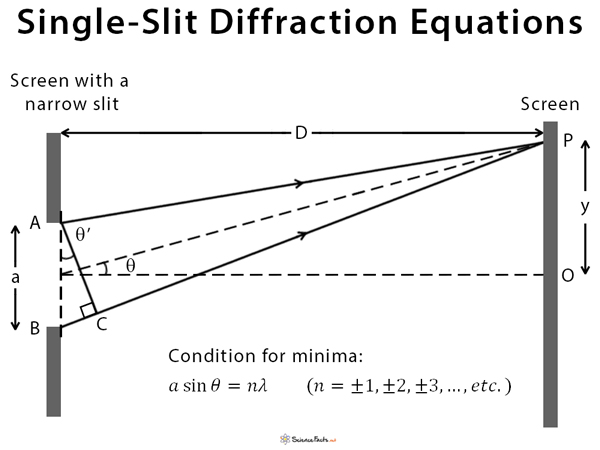
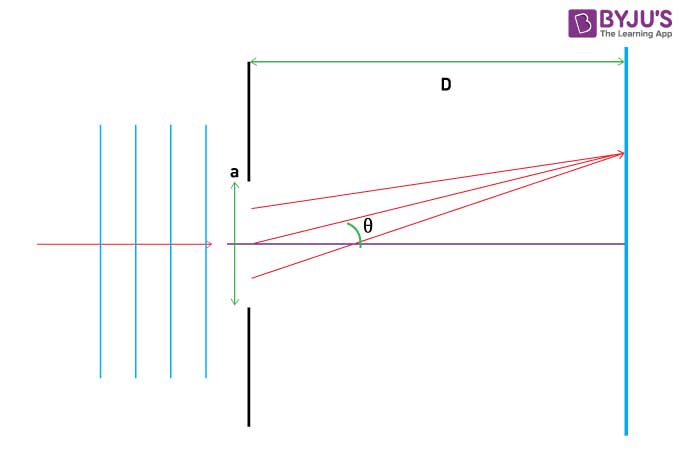
In other words, the locations of the interference fringes are given by the equation d sin θ = m λ d sin θ = m λ, the same as when we considered the slits to be point sources, but the intensities of the fringes are now reduced by diffraction effects, according to Equation 4.4. The diffraction pattern of two slits of width a that are separated by a distance d is the interference pattern of two point sources separated by d multiplied by the diffraction pattern of a slit of width a. Although the details of that calculation can be complicated, the final result is quite simple: This gives the intensity at any point on the screen. That is, across each slit, we place a uniform distribution of point sources that radiate Huygens wavelets, and then we sum the wavelets from all the slits. To calculate the diffraction pattern for two (or any number of) slits, we need to generalize the method we just used for a single slit. In this section, we study the complications to the double-slit experiment that arise when you also need to take into account the diffraction effect of each slit. However, if you make the slit wider, Figure 4.10(b) and (c) show that you cannot ignore diffraction. Therefore, it was reasonable to leave out the diffraction effect in that chapter. If the slit is smaller than the wavelength, then Figure 4.10(a) shows that there is just a spreading of light and no peaks or troughs on the screen. We assumed that the slits were so narrow that on the screen you saw only the interference of light from just two point sources. When we studied interference in Young’s double-slit experiment, we ignored the diffraction effect in each slit.


 0 kommentar(er)
0 kommentar(er)
